(Taking small liberties with the types.-)
the toy e.g. (5 attributes)
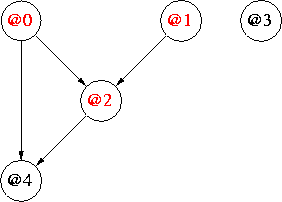
An Inferred Bayesian Network
details of the network's nodes next...
{CTleaf N(1.0,0.41)(+-0.1),_,_,_,_}, --@0
{CTleaf _,mState[0.5,0.5],_,_,_}, --@1
{CTfork @0<|>=1.4[ --@2|@0,@1
{CTleaf _,_,mState[0.99,0.01],_,_},
{CTfork @1=False|True[
{CTleaf _,_,mState[0.98,0.02],_,_},
{CTleaf _,_,mState[0.02,0.98],_,_}]}]},
{CTleaf _,_,_,mState[0.5,0.5],_}, --@3
{CTfork @2=False|True[ --@4|@0,@2
{CTfork @0<|>=1.0[
{CTleaf _,_,_,_,N(0.55,0.2)(+-0.1)},
{CTfork @0<|>=1.4[
{CTleaf _,_,_,_,N(1.0,0.2)(+-0.1)},
{CTleaf _,_,_,_,N(1.45,0.2)(+-0.1)}]}]},
{CTleaf _,_,_,_,N(3.45,0.2)(+-0.1)}]}
N.B. Don't get the nodes of the network and
of a tree confused!Components
mState[p0,p1,...] -- multi-state distribution[*].
N(m,s) -- normal (Gaussian) distribution[*].
"classification" tree[*],
CTleaf -- model[*] an attribute,
CTfork -- test[*] an attribute.
([*] message lengths, i.e. complexities, direct search & prevent over-fitting.)
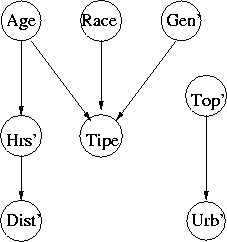
2. A Real Example: Lost Person
data Tipe = Alzheimers | Child | Despondent | Hiker | ...
type Age = Double
data Race = White | Black deriving (Eq, Enum,...
data Gender = Male | Female deriving (Eq, Enum,...
data Topography = Mountains | Piedmont | Tidewater deriving...
data Urban = Rural | Suburban | Urban deriving (Eq,Ord,...
type HrsNt = Double -- hours notified
type DistIPP = Double -- distance
...
Estimators
type MissingPerson = (Maybe Tipe, Maybe Age, ...)
e0 = (estModelMaybe estMultiState) --Tipe
e1 = (estModelMaybe (estNormal 0 90 1 70 0.5)) --Age
...
e7 = (estModelMaybe (estNormal 0 50 0.5 30 0.2)) --DistIPP
estimator = estVariate15 e0 e1 e2 e3 e4 e5 e6 e7 e8 e9 e10 e11 e12 e13 e14
NB. There is(n't:-) a lot of missing data.
1st Inferred Network for
Inferred Network's Trees...
Net:[
-- @1, Age:
{CTleaf _,(Maybe 50:50,N(40.6,27.5)... },
... etc. ...
-- @6, HrsNt:
{CTfork @1(<|>=62.0|?)[
{CTleaf...,(Maybe 50:50,N( 8.7, 7.6)...},
{CTleaf...,(Maybe 50:50,N(21.4,26.3))...},
{CTleaf...,(Maybe 50:50,N(20.0,..1-case)..}
]},
... ]
network: 115.1 nits + data: 5396.6 nits
null: 5935.6 nits (@0..@7)
E.g. A High-Order Function of an Estimator
estModelMaybe estModel dataSet =
let
present (Just _) = True
present Nothing = False
m1 = uniformModelOfBool -- [*]
m2 = estModel (map (\(Just x) -> x)
(filter present dataSet))
in modelMaybe m1 m2
[*] or if modelling missing-ness...
m1 = estMultiState (map present dataSet)
Classes e.g.
class Project t where -- as in `projection' select :: [Bool] -> t -> t selAll :: t -> [Bool] -- all True flags
A type, t, in class Project
can be projected onto a
select-ed sub-space.
E.g. A 15-dim'n estimator, such as estVariate15 e0...e14.
Also a related class for select-ive partitioning of data within trees.
print warning: May lose network's lines if shrunk.| e.g. |
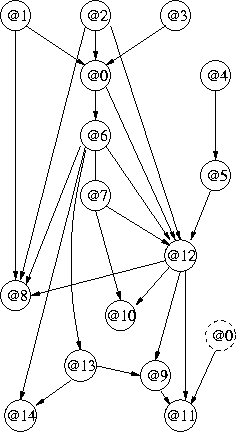 |
| |||||||||||||||||||||||||||||||||||||||||||||||
|
A Network Inferred for all 15 Attributes of `lost persons' | |||||||||||||||||||||||||||||||||||||||||||||||||
Summary
Have types and type-classes for Models, Function-Models and Time-Series models. Polymorphic types, type classes, high-order functions, lazy-evaluation -- all useful.
Easy to write a new model,
Other case studies include -- mixture models (clustering), time-series, Markov models, mixtures of Markov models, function models (regressions), etc..
[1] L. Allison. Types and classes of machine learning and data mining. 26th Australasian Computer Science Conference (ACSC), Adelaide, pp.207--215,L. Allison. Inductive inference 1.
L. Allison. Models for machine learning and data mining in functional programming. J. Functional Prog. 15(1) pp.15-32
R. J. Koester. Virginia dataset on lost-person behaviour.
S. Peyton-Jones & others. Report on the Programming Language Haskell-98.
C. R. Twardy. SARbayes: Predicting lost person behavior. Presented to National Association of Search and Rescue (NASAR), Charlotte, 2002.
C. R. Twardy & L. Hope. Missing data on missing persons. submitted 2004.
© L. Allison, School of Computer Science and Software Engineering, Monash University, Australia 3800. Created with "vi (Linux & Solaris)", charset=iso-8859-1