[01]
>>
Segmentation of Ordered Data
On work by Leigh Fitzgibbon
Other debts (lacitebahpla order):
Chris Wallace,
Jon Oliver,
Dean McKenzie,
David Dowe,
Rohan Baxter
© 2001, Lloyd Allison,
School of Computer Science and Software Engineering,
Monash University, Australia 3168
See:
L. J. Fitzgibbon, L. Allison & D. L. Dowe.
Minimum message length grouping of ordered data.
Proc. 11th Int. Workshop on Algorithmic Learning Theory
(ALT'2000)
pp56-70, Sydney, LNCS V1968, Springer-Verlag,
December 2000
This
document is online at
users.monash.edu/~lloyd/Seminars/Series-Seg01/index.shtml
and contains hyper-links to more detailed notes on certain topics and
to some of the references.

<<
[02]
>>
Problem
- Given a sequence, s1, ..., sn, of multivariate data,
- divide it into k segments (i.e. k-1 cut-points)
- that best describe the data
- a difficult problem if data ranges of neigbouring segments overlap.
Simplest model: One segment.
Most complex model: One segment per element (over-fitting).

<<
[03]
>>
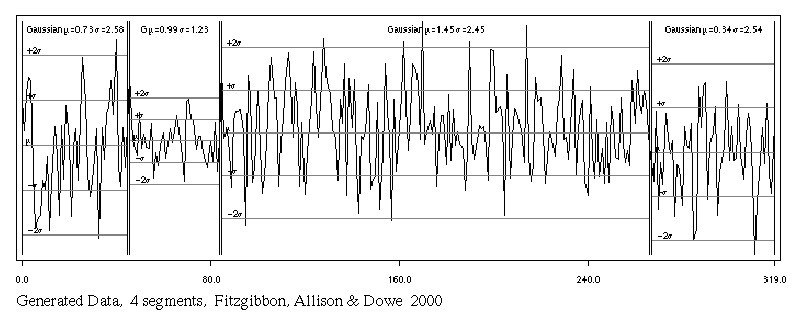
e.g. Generated data, 4 segments, 3 cut-points, means & S.D.s shown

<<
[04]
>>
Fisher's Algorithm (1958)
Dynamic Programming:
- Given k,
- if c1, c2, ..., ck-1
are k-1 optimal cut-points for s1, ..., sik-1
- then c1, c2, ..., ck-2
are k-2 optimal cut-points for s1, ..., sik-2
so
- compute optimal 1_segmentations for s1, .., si,
for all i=1..n
- iteratively
- compute optimal k_segmentations from the optimal k-1_segmentations
- to some maximum value K
O(K*n2)-time.

<<
[05]
>>
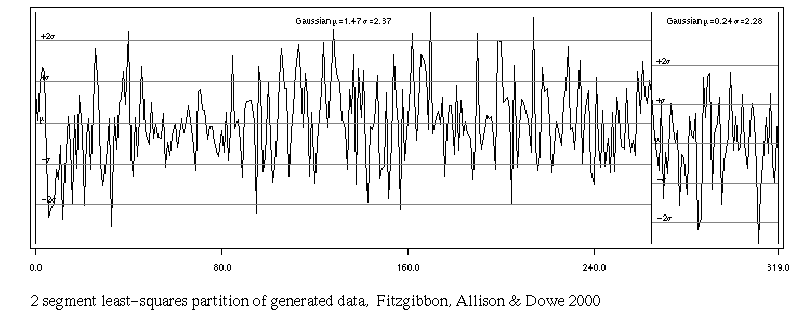
2 segments, Least Squares
finds one cut point well

<<
[06]
>>
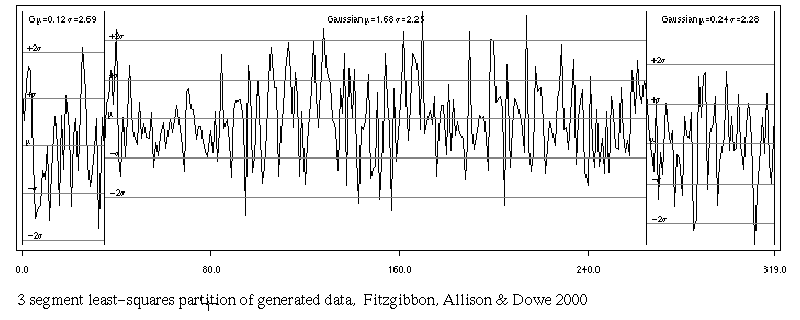
3 segments LSq
2nd cut point is close

<<
[07]
>>
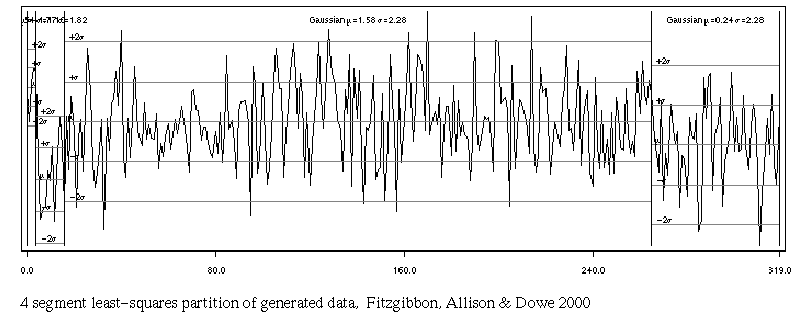
4 segments LSq
two small segments inappropriately inferred

<<
[08]
>>
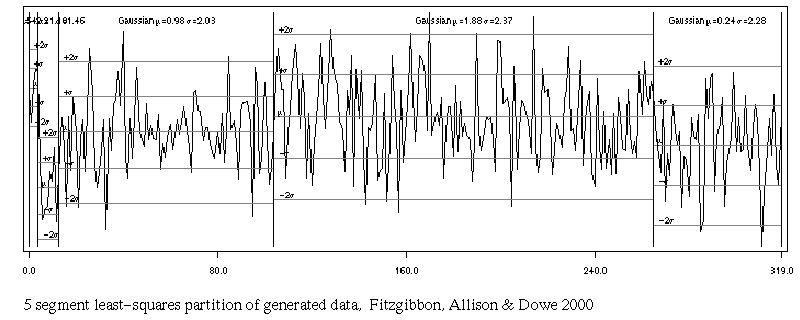
5 segments LSq
two cut points poor, one fair, one good

<<
[09]
>>
Stopping
But Fisher's algorithm (1958) has no stopping criterion:
Least squares differences (say) decrease as k-->n.
Solution: Model has a message length (cost) . . .
- [Integer] # segments
- Cut-point positions to appropriate accuracy
- For each segment: its parameters to appropriate accuracy
- NB. Can get ``sufficient statistics'' for i..j from
those for 1..i-1 and for 1..j.
This prevents over-fitting.

<<
[10]
>>
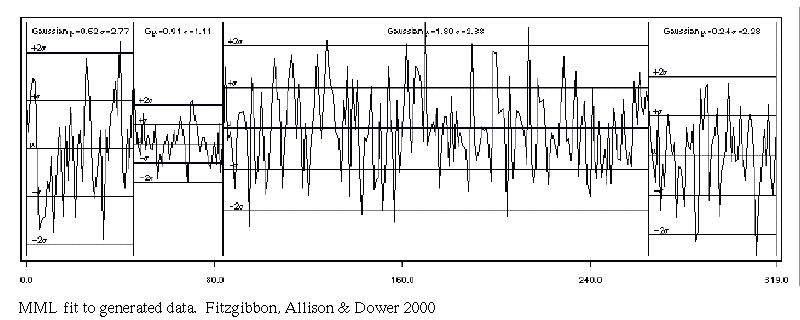
MML fit:
essentially correct

<<
[11]
>>
Real-World Data, MML:
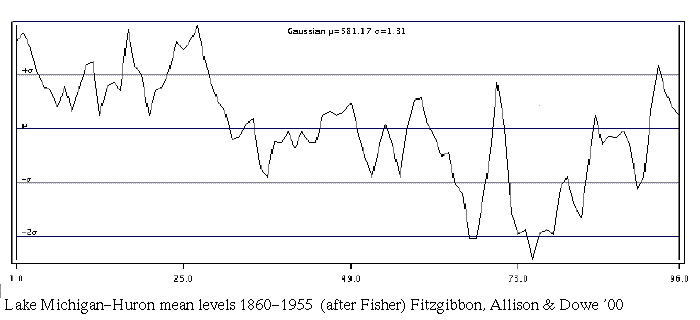
W. Fisher's data:
96 years of Lake Michigan Huron

<<
[12]
>>
Real-World Data, MML:
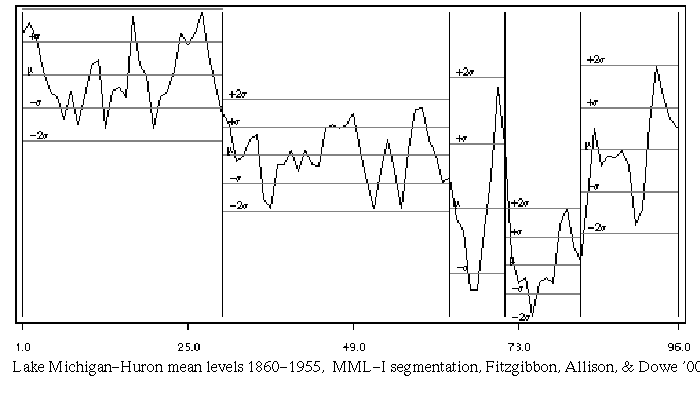

<<
[13]
>>
MML:
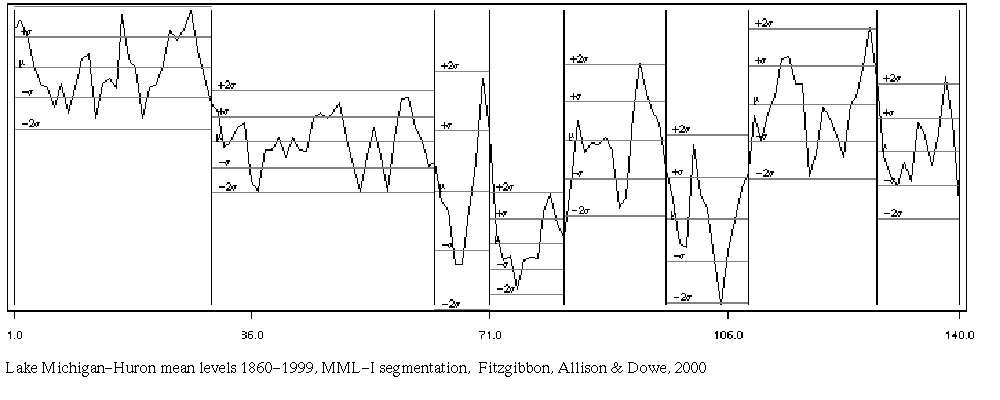
140 years of lake levels . . .

<<
[14]
Summary
- Minimum Message Length gives a stopping criterion (no overfitting).
- Time Complexity O(K.N2)
where K is max # of segments considered
References
- W. D. Fisher.
On grouping for maximum homogeneity.
Jrnl. Am. Stat. Soc. 53 pp789-798 1958.
Dynamic programming algorithm, no stopping criterion.
- R. A. Baxter & J. J. Oliver.
The kindest cut: minimum message length segmentation.
Proc. 7th Int. Workshop on Algorithmic Learning Theory
pp83-90, LCNS V1160, Springer-Verlag, 1996.
Binary data, investigates precision of
stating cut-points
- L. J. Fitzgibbon, L. Allison & D. L. Dowe.
Minimum message length grouping of ordered data.
Proc. 11th Int. Workshop on Algorithmic Learning Theory (ALT'2000),
pp56-70, Sydney, LNCS V1968, Springer-Verlag,
December 2000.
Multivariate data, dynamic programming algorithm,
avoids stating cut-points!
- Data:
[1860-1955] ++
[1918-1999] ==>
[1860-1999]