Edit Distance

"Lazy-evaluation in a functional language is exploited to make the simple dynamic-programming algorithm for the edit-distance problem run quickly on similar strings: being lazy can be fast." [Inf. Proc. Lett., 43(4), pp207-212, Sept' 1992].

a = acgtacgtacgt
b = acatacttgtact

a = acgtac  gtacgt
    || |||  |||| |
b = acatacttgtac t
      ^   ^^    ^
      |   ||    |
      |   ||    delete
      |   ||
      |   insert*2
      |
      change

d a b = 4

The algorithm below organises the edit distance "matrix" by diagonals, not by rows or columns. Its time-complexity is O(n×d) where n is the length of the sequences and d is the edit distance between them, i.e. it is fast if the sequences are similar, d<<n. The original program was in Lazy ML; it is given in Haskell 98 here:

module Edit_IPL_V43_N4 (d) where
-- compute the edit distance of sequences a and b.
d a b =
 let 
   -- diagonal from the top-left element
   mainDiag = oneDiag  a b (head uppers) ( -1 : (head lowers))

   -- diagonals above the mainDiag
   uppers   = eachDiag a b (mainDiag : uppers)

   -- diagonals below the mainDiag
   lowers   = eachDiag b a (mainDiag : lowers)  -- !

   oneDiag a b diagAbove diagBelow =  -- \   \   \
    let                               --  \   \   \
      doDiag [] b nw n w = []         --   \  nw   n
      doDiag a [] nw n w = []         --    \   \
      doDiag (a:as) (b:bs) nw n w =   --      w   me
       let me = if a==b then nw       -- dynamic programming DPA
                else 1+min3 (head w) nw (head n)
       in  me : (doDiag as bs me (tail n) (tail w))

      firstelt = 1+(head diagBelow)
      thisdiag =
        firstelt:(doDiag a b firstelt diagAbove (tail diagBelow))

    in thisdiag

   min3 x y z =
   -- see L. Allison, Lazy Dynamic-Programming can be Eager
   --     Inf. Proc. Letters 43(4) pp207-212, Sept' 1992
     if x < y then x else min y z   -- makes it O(|a|*D(a,b))
     -- min x (min y z)             -- makes it O(|a|*|b|)
   -- the fast one does not always evaluate all three values.

   eachDiag a [] diags = []
   eachDiag a (b:bs) (lastDiag:diags) =
    let nextDiag = head(tail diags)
    in  (oneDiag a bs nextDiag lastDiag):(eachDiag a bs diags)

   -- which is the diagonal containing the bottom R.H. elt?
   lab = (length a) - (length b)

 in last( if      lab == 0 then mainDiag
          else if lab > 0 then lowers !! ( lab-1)
          else                 uppers !! (-lab-1) )

 -- module under Gnu `copyleft' GPL General Public Licence.

The code above calculates the value of the edit distance between the sequences a and b only. The "matrix" does contain enough information to recover an alignment of a and b that achieves this value, but this is left as an exercise.

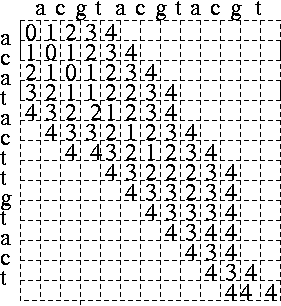
-- Evaluating O(n×d) entries --