Some of these classes we've encountered before, others we'll encounter shortly. Others you'll need to check up in your text book!

A few notes on the classes...

Font provides font manipulation methods.

Fontmetrics provides a means to work out the height and width of particular characters of a particular font drawn on a particular screen and other font-specific attributes.

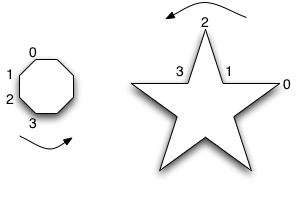
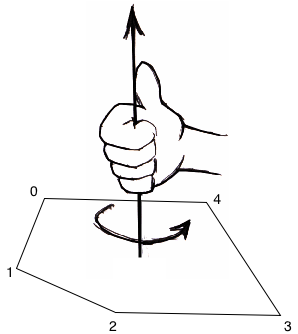
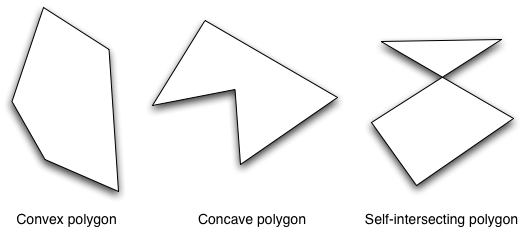
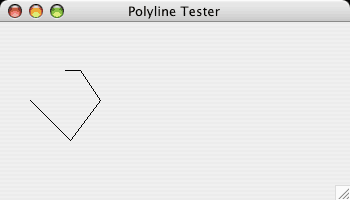
Polygon (as its name implies) provides methods for drawing... polygons!

BasicStroke is provided for line drawing.

GradientPaint and TexturePaint are for filling shapes with colours and patterns.

A number of classes exist in Java for creating 2D shapes (e.g. Arcs, Ellipses, Rectangles etc.)

The Graphics2D class is a sub-class of Graphics. Look back at the code of last lecture and you'll notice that a Graphics2D object was used. Graphics2D provides some new 2D graphics capabilities over and above those provided by the basic Graphics class.

import java.awt.*;
import java.awt.event.*;
import javax.swing.*;

public class FontTest extends JFrame
{
   public FontTest ()
   {
      super ("The Super Font Tester");
      addWindowListener(new WindowAdapter() { public void windowClosing(WindowEvent e) { System.exit(0); } });
      setSize(420, 125);
      setVisible(true);
   }
   
   public void paint(Graphics g)
   {
      g.setColor( Color.red );
      g.setFont( new Font ("Serif", Font.BOLD, 12) );  // serif font in bold, 12 point
      g.drawString("Serif 12 point bold", 20, 50);
   
      g.setColor( Color.blue );
      g.setFont( new Font ("Monospaced", Font.ITALIC, 24) );  // monospaced font in italic, 24 point
      g.drawString("Monospaced 24 point italic", 20, 70);
   
      g.setColor( Color.black );
      g.setFont( new Font ("SansSerif", Font.PLAIN, 14) );    // sans-serif font in plain, 14 point
      g.drawString("Sans-serif 14 point plain", 20, 90);
   
      g.setColor( Color.green );
      g.setFont( new Font ("Serif", Font.BOLD + Font.ITALIC, 18) );
      g.drawString(g.getFont().getName() + " " + g.getFont().getSize() + " point bold, italic", 20, 110);
   }
   
   public static void main (String args[])
   {
      FontTest newFontWindow = new FontTest();
   }
}

A closed shape whose boundary consists of a set of straight edges is called a polygon.

By convention vertices of a polygon ought to be specified in an anticlockwise order around the edge of the shape as a series of co-ordinates.

Right-hand rule for polygon front face determination

The ordering of vertices doesn't matter too much for a 2D polygon but becomes important when doing 3D graphics.

The front of a polygon in 3 dimensions is determined according to a right hand rule:

Curl the fingers of your right hand from the first vertex on the boundary, through the second and third vertices. Your right thumb now acts as a surface normal vector from the front of the polygon.

A convex polygon has no internal angle greater than 180 degrees.

A concave polygon has at least one internal angle greater than 180 degrees.

It is also possible to define self-intersecting polygons where edges cross over one another. Be aware that these polygons sometimes cause problems for graphics rendering software and may not always be displayed correctly.

// A polygon drawing example...

import java.awt.*;
import java.awt.event.*;
import javax.swing.*;

public class PolygonTest extends JFrame
{
   public PolygonTest ()
   {
      super ("Polygon Tester");
      addWindowListener(new WindowAdapter() { public void windowClosing(WindowEvent e) { System.exit(0); } });
      setSize(350, 200);
      setVisible(true);
   }
   
   public void paint(Graphics g)
   {
      int xCoordinates[] = { 30, 70, 100, 80, 65 };
      int yCoordinates[] = { 100, 140, 100, 70, 70 };

      Polygon shape1 = new Polygon( xCoordinates, yCoordinates, 5 );
      g.drawPolygon(shape1);
   
      int xCoordinates2[] = { 130, 170, 200, 180, 165 };
      int yCoordinates2[] = { 100, 140, 100, 70, 70 };
   
      g.drawPolygon(xCoordinates2, yCoordinates2, 5);
   
      Polygon shape2 = new Polygon( );
      shape2.addPoint( 230, 100 );
      shape2.addPoint( 270, 140 );
      shape2.addPoint( 300, 100 );
      shape2.addPoint( 280, 70 );
      shape2.addPoint( 265, 70 );
      g.fillPolygon(shape2);
   }
   
   public static void main (String args[])
   {
      PolygonTest newPolygonWindow = new PolygonTest();
   }
}

The output of the above program.

Note that the drawing routines automatically close the polygon from the last point specified, back to the first point specified.

// A polyline drawing example...

import java.awt.*;
import java.awt.event.*;
import javax.swing.*;         

public class PolylineTest extends JFrame
{
   public PolylineTest ()
   {
      super ("Polyline Tester");
      addWindowListener(new WindowAdapter() { public void windowClosing(WindowEvent e) { System.exit(0); } });
      setSize(350, 200);
      setVisible(true);
   }
   
   public void paint(Graphics g)
   {
      int xCoordinates[] = { 30, 70, 100, 80, 65 };
      int yCoordinates[] = { 100, 140, 100, 70, 70 };

      g.drawPolyline(xCoordinates, yCoordinates, 5);
   }
   
   public static void main (String args[])
   {
      PolylineTest newPolylineWindow = new PolylineTest();
   }
}

The output of the above program.

Note that the drawing routine does not automatically close the shape from the last point specified, back to the first point specified.

Graphics2D g2d;

g2d.translate (xTranslation, yTranslation); // parameters: two ints to translate the current origin to a new location
g2d.rotate (thetaRotation); // parameter: one double for a rotation about the origin in *radians*
g2d.scale (xScale, yScale); // parameters: two doubles to resize the drawing relative to the previous size