^up^
[01]
>>
(Decision) Classification Trees I
Problem:
Given multivariate data, each item having n-attributes
@1, @2,... @n,
infer a tree that models
the dependent attribute
@n, say, given
input attributes @1 ... @n-1.
Model
A tree of
- fork nodes,
which split data, specify tests on input attributes, and
- leaves, which model dependent attribute.
Applications
Expert systems: Examples are given, e.g. case histories
or expert judgement, the learned Tree mimics expert behaviour.
Consider binary attributes first, n-ary and
continuous attributes later.
This
document is online at
http://www.csse.monash.edu.au/~lloyd/Archive/2005-08-Tree01/index.shtml
and contains hyper-links to other resources.

<<
[02]
>>
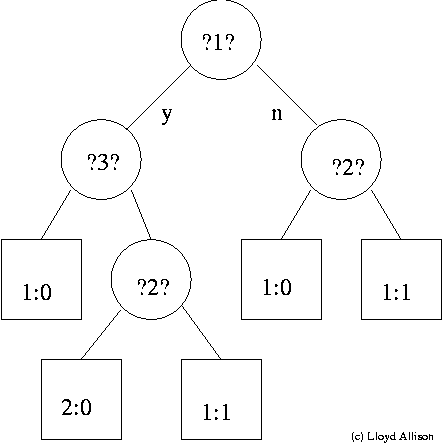
e.g. my car won't start
Engine turns over but will not run.
?Is it a problem with the ignition system
(spark plugs, leads, coil, distributor or equivalent)?
We have a training set of cases, i.e. examples:
| | 1: engine fires | 2: clicking noise | 3: petrol smell | 4: ignition problem | note |
| 1: | y | n | n | n | fuel |
| 2: | y | n | n | y | plugs |
| 3: | y | y | n | y | leads |
| 4: | n | y | n | y | leads |
| 5: | y | n | y | n | flooded |
| 6: | n | n | y | n | leak |
| 7: | n | n | y | y | plugs |
| 8: | y | y | n | y | |
| | etc. | ... | ... | ... | |
| | . . . etc. . . . |
Prediction (of @4) must be probabilistic, see cases 6 and 7.

<<
[03]
>>
Simplest Tree:
a single leaf node.

<<
[04]
>>
A Complex Tree:
How can we compare a simple tree v. a complex tree fairly?

<<
[05]
>>
Model (i.e. Tree) Selection
Bayes:
P(Data&Tree) = P(Tree) × P(Data|Tree)
MsgLen(Data&Tree) = MsgLen(Tree) + MsgLen(Data|Tree)
A simple tree has a high prior probability,
i.e. a short message length.
A complex tree has a low prior probability,
i.e. a long message length.
These quantities are commensurable with msgLen(Data|Tree),
i.e. the fit.
This gives a trade-off.

<<
[06]
>>
Complexity, i.e. Message Length, of a Tree
Deal with this in 3 parts
- topology,
- for each fork: split attribute,
- for each leaf: distribution parameters.

<<
[07]
>>
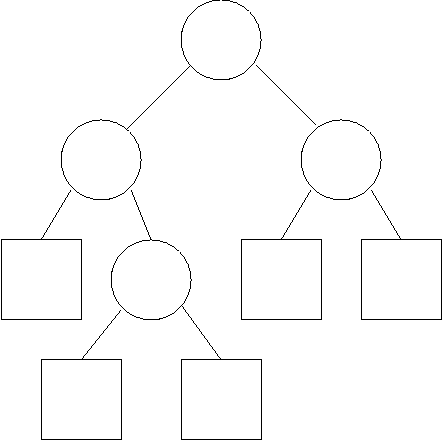
1. Tree Toplogy:
Traverse Tree in prefix-order, write `F' for a fork (split)
and `L' for a leaf:
F F L F L L F L L

<<
[08]
>>
F F L F L L F L L
- NB. It is well known that every
binary tree
has exactly one more leaf node than it has forks.
- Set P(F) = P(L) = 0.5
- e.g. The given tree topology costs 9 bits.
- Can detect the end of the code when #L = #F+1

<<
[09]
>>
2. Split Attributes:
- It takes -log2(#a) bits
to specify one of #a attributes,
- assuming all are equally likely,
- e.g. log2(3) bits for the root node and the given tree.
- A split attribute in a fork-node cannot be re-used in a subtree.
- e.g. log2(2) = 1 bit for the next split attribute
- and -log2(1) = 0 bits for a 3rd-level split.
- e.g. Total
= log2(3) + 2×log2(2) + log2(1)
= log2(3) + 2 bits

<<
[10]
>>
3. Leaf Distributions:
- A
binomial distribution
is used for a binary attribute, @predicted.
- State one parameter, i.e. P(@predicted)=T,
to optimum, finite accuracy
3'. An alternative view
- Do not code an explicit distribution in a leaf,
- instead use the adaptive coding method
for items arriving at the leaf,
- simple & data message length is a fraction of a bit less per leaf.
(Essentially equivalent.)

<<
[11]
>>
Data Given Tree (Model)
NB. Only applies to predicted attribute(s),
input attributes are given, i.e. common knowledge.
(# @predicted = T) × -log2 P'(T)
+ (# @predicted = F) × -log2(1-P'(T))
The MML estimator for a
2-state
distribution is:
P'(T) = (#Tobs + 1/2) / (#Tobs + #Fobs + 1)
P'(F) = (#Fobs + 1/2) / (#Tobs + #Fobs + 1)

<<
[12]
>>
Conclusions
- Tree consists of fork-nodes (splits, tests) and leaf distributions
- Tree message length (cost)
- topology
- for each fork: split attribute
- for each leaf: distribution parameters
- Data message length (cost) given Tree
- item cost given 2-state (or multi- etc.) in selected leaf
- allows simple trees and complex trees to be compared fairly.
Generalizes to
multi-state
(>2) and
continuous
attributes,
etc..