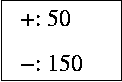
1. (a) Define the following terms as they apply to learning and prediction:
(b) Three fair coins, Pr(H)=0.5, and one biased coin, Pr(H)=0.75,
are placed in a cloth bag;
all of the coins are identical in appearance and in weight.
The bag is shaken and one coin is drawn out.
The selected coin is thrown four times with
these
2. (a) For multi-state probability distributions, define the `Kullback Leibler' (KL) distance from the "true" probability distribution P1 to another probability distribution P2.
(b) Below are two probability distributions, P and Q, over {A,C,G,T}. Calculate the KL distance from P to Q, and also from Q to P.
| - | A | C | G | T |
| P: | 1/2 | 1/4 | 1/8 | 1/8 |
| Q: | 1/8 | 1/2 | 1/4 | 1/8 |
3.
A library has a collection of 50 essays,
all believed to have been written by author X.
Professor Smith disagrees and believes that
some of the essays were written by another person, author Y.
Unfortunately
no work exists that is absolutely certain to have been written by X, and
no work exists that is absolutely certain to have been written by Y.
It is assumed that each essay had a single author.
It is a fact that different people tend to use words,
including common words, with different frequencies.
Smith gathers data from the essays,
specifically the length of each essay and the number of times that
each of the following common words appears in each essay:
(a) How would you apply Snob to this problem and this data? Why?
(b) What signs would you look for in Snob's results to support the single-author hypothesis, or to support the two-author hypothesis, or other possible explanations of the data? Why?
4.
(a) Consider decision- (classification-) trees over multivariate data
with discrete and/or continuous attributes to be tested
and a discrete (`class') attribute to be predicted.
Describe an efficient scheme to encode
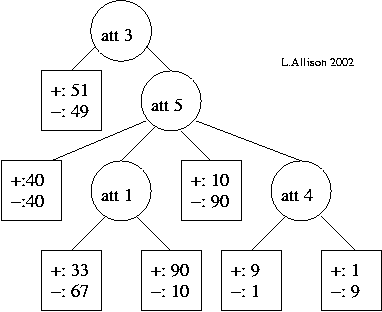
If tree 1 and tree 2, below, are two possible models of the data, which tree is the better explanation of the data? Why?
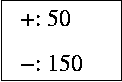
|

|
| tree 1 | tree 2 |
|---|---|
| (The leaf nodes show the frequencies of positive and negative cases.) | |
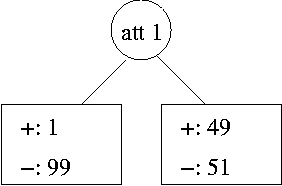
(c) More data of the same kind is collected and the following tree structure, including splits, is learned:
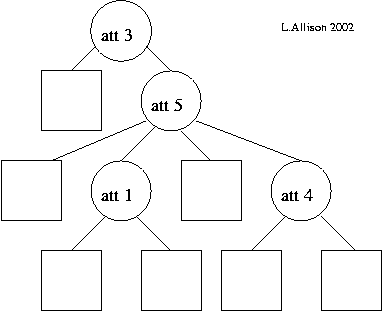
(d) The tree models the new data as follows: