1. (a) Briefly,
define the following terms as they apply in
- Joint probability.
- Independent (as used with probability).
- Bayes's theorem.
- Information.
[10 marks]
(b) Four tetrahedral dice are placed in a cloth bag.
The dice are identical in appearance and in weight.
Three of the dice are unbiased,
- What is the prior probability of a fair dice versus a biased dice?
- What is the likelihood of 1,4,1,2 for a fair dice, and for a biased dice?
- What is the posterior probability of a fair dice versus a biased dice?
[10 marks]
2. (a) For a multi-state probability distribution, P(.), define how to calculate the `Entropy', and give an explanation of what the quantity represents.
(b) What is the entropy of the following distribution for a 6-sided dice?
| 1 | 2 | 3 | 4 | 5 | 6 |
| 1/2 | 1/4 | 1/16 | 1/16 | 1/16 | 1/16 |
(c) For multi-state probability distributions, define the `Kullback Leibler' (KL) distance from the "true" probability distribution P(.) to another probability distribution Q(.).
(d) Below are two probability distributions, P and Q, for dice.
Calculate the KL distance from P
| 1 | 2 | 3 | 4 | 5 | 6 | |
| P: | 1/6 | 1/6 | 1/6 | 1/6 | 1/6 | 1/6 |
| Q: | 1/2 | 1/4 | 1/16 | 1/16 | 1/16 | 1/16 |
|
3. You are observing a multi-player game that is played with a silver coin, `S', and a gold coin, `G'. Each turn involves throwing the two coins. You notice that <H,H> and <T,T> seem to occur rather often and <H,T> and <T,H> rather infrequently. You watch the game, collect some data on the coins (right) and decide to use MML to analyse it (of course a real data set would be much larger). (a) You model the data as a mixture of one or more classes.
Each class is defined by a bivariate model.
Each bivariate model consists of two 2-state distributions, i.e.
one 2-state distribution for S and another for G. [15 marks]
(b) One could convert the data as follows: <H,H> -->0, <H,T> -->1, <T,H> -->2, <T,T> -->3 and could model the transformed univariate data by a 4-state distribution. In this case, does it now make sense to talk about a one-class v. a two-class model, or not? If so, why and what are the consequences, otherwise why not? [5 marks]
|
|
(a) Data nicely arranged for Snob:
`trial' is the `thing' number,
`S' is attribute 1, and
`G' is attribute 2.
You could try the data through Snob
(replicate the data a few thousand(?) times
to a realistic size).
The 1-class model will have
<Pr(S=H)=0.5, Pr(G=H)=0.5>.
(The factorial method lets you estimate the cost of model and data.)
The 2-class model can bias class-1, say, towards <H,H> and
class-2 towards <T,T>.
Put in some plausible numbers and . . .
(b) No: Note that a mixture of two or more 4-state distributions is a 4-state distribution. They are indistinguishable. (The same is not true of mixtures of Normal distributions, for example.)
4.
(a) Consider classification- (decision-) trees over multivariate data
with discrete and/or continuous attributes to be tested
and a discrete (`class') attribute to be predicted.
Describe an efficient scheme to encode
- A multivariate data set has the following attributes:
- att 1: M, F -- gender.
- att 2: continuous -- age measured to one decimal(!) place, e.g. 42.3.
- att 3: g, v, w, j -- 4 possible values.
- att 4: boolean
- att 5: boolean -- the `class', i.e. the attribute to be predicted.
- att 2: continuous -- age measured to one decimal(!) place, e.g. 42.3.
- There are 661 data items.
(b) Describe the encoding of the following tree (without data) in reasonable detail, and estimate its message length. Show working. State any assumptions.
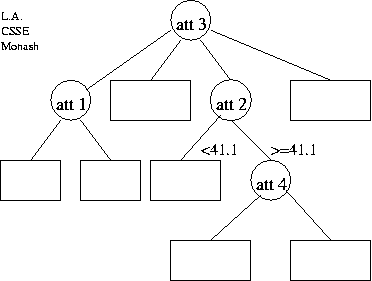
(c) The flow of the data
through the tree is shown in the diagram below.
Estimate the message length of (attribute 5 of)
the data in each of the two leaf nodes
below the node that tests
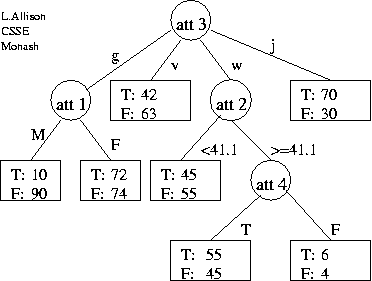
(d) Estimate the change in total message length
(both tree and data|tree)
if the two leaves and the att 1 test-node,
as identified in part (c),
were collapsed to one leaf; show working.
© 6/2003, L. Allison, School of Computer Science and Software Engineering, Monash University, Australia 3800. Created with "vi (Linux & IRIX)", charset=iso-8859-1
Note that attribute 2 is continuous, i.e. it could be "reused",
that is tested multiple times in a path from the root to a leaf.
The cost of transmitting a cut-point, such as `41.1', depends on
whether it is the median (1-bit), a quartile (3-bits),
an octile (5-bits), etc.,
of the subset of the data reaching that test.
Note that attribute 3 is 4-valued, and that using 1-bit for fork/leaf is only optimal for binary trees.