- 4. A data-set has the following attributes:
You want to infer a classification tree to predict@0, Gender = Male | Female @1, Married = W | S @2, Party = Lib | Lab | Dem | Green | Indep @3, SEG = L | M | H @4, Z = P | N -- predict @4 Z from @0 to @3. - (a)
Briefly describe a general and efficient scheme for
encoding classification trees over
discrete and/or continuous input attributes, and
discrete outputs.
[(a) 6 marks]
- (b) Show how the structure of the following tree would be encoded (without data), and estimate its message length. Show working.
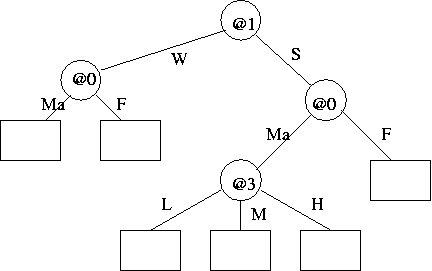 [(b) 6 marks]
[(b) 6 marks]- (c) The flow of data through the tree is shown below. Estimate the message length of the data (i.e. @4, Z) in the
(d) You are only now told that @3, SEG, is an ordered discrete type,left-most leaf. Show working.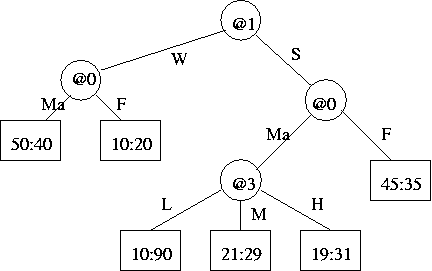 [(c) 6 marks]
[(c) 6 marks]i.e. L < M < H, it shares this (<) property of continuous attributes. This means that instead of 3-way splits, 2-way splits could be used on @3 SEG,i.e. {L} v. {M,H}, and {L,M} v. {H}. How would the tree encoding scheme be changed to deal efficiently with this new kind of attribute and split?[(d) 8 marks]- (e) Draw a new subtree that uses these new 2-way splits and is otherwise equivalent to (has the same leaves as) the subtree rooted at the old 3-way
split in (c). What would the change in the total message length of tree and data be compared to the original scheme as used in part(a) to part(c)? Show working.[(e) 7 marks]- (f) You will notice that in the new subtree you drew for part(e) the distributions of Z are very similar when SEG=M or when SEG=H. Estimate the change in the total message length if those two leaves of the new subtree are collapsed into one. Show working.
[(f) 7 marks][(total) 40 marks] - (b) Show how the structure of the following tree would be encoded (without data), and estimate its message length. Show working.
© 6/2003, L. Allison, School of Computer Science and Software Engineering, Monash University, Australia 3800.
(a) Topology [how?], tests [how?].
Arity re tests on discrete attributes [how?].
Parameters of leaf distributions.
Data (predicted) attribute(s) according to selected leaf model.
Don't forget, if a test-node tests a continuous attribute,
that attribute can still be re-tested in subtrees of the test-node.
(And looking ahead, you will have to quantify either
the leaf parameter cost or, easier, the adaptive code (see Q2)
under part(c).)
(b) Note that SEG's arity (three), doubtless as
described for discrete tests in the answer to part(a), comes into play
for the children of the test-node for @3.
See the [tables]
for log2 and/or
(c) Like Q2, except it is a simpler 2-state {P|N} distribution here,
(d) This makes SEG "like" a continuous attribute in some ways.
If tested, it is also necessary to code (1-bit for 3-state SEG)
what the test condition is,
(e) Here is the "the subtree rooted at the old 3-way split"
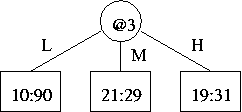
There are two possible trees that "use[s] these new 2-way splits" and are "otherwise equivalent to (have[s] the same leaves as)" it. Either one of the following would do:
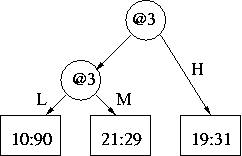 | or | 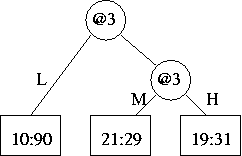 |
(f) And here is the subtree if "those two leaves [when SEG=M, SEG=H] of the new subtree are collapsed into one."
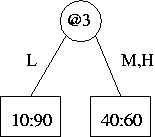
Under topology, we save one new-style split node on @3 and one leaf.
The data part must change slightly corresponding to the move from
(Sanity check:
100 data in the ratio 40:60 must cost very roughly 100-bits, 69-nits,