- 4.Consider classification- (decision-) trees over multivariate data with
discrete and/or continuous attributes to be tested and
a discrete ('class') attribute to be predicted.
-
- (a) Describe an efficient scheme to
encode (i) a tree, and (ii) the data given the tree.
[(a) 10 marks]
-
- A certain data set has the following attributes:
@0, Gender = Male | Female
@1, Party = Lib | Dem | Lab | Green
@2, Seg = U | V | W
@3, Age is continuous
@4, Z = P | N -- the 'class' to be predicted.
- Although Age is continuous it just happens that
eleven distinct values appear, each several times, in the data set:
19, 24, 26, 32, 37, 45,
48, 57, 65, 69 and 73.
-
-
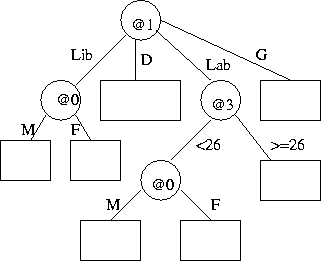
- (b) Describe
the encoding of the following tree (without data)
in reasonable detail, and estimate its message length.
Show working. State any assumptions.
[(b) 10 marks]
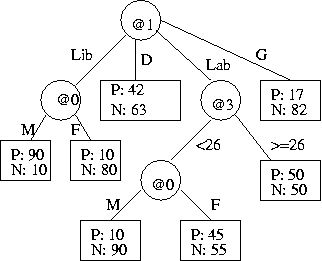
- (c) The flow of the data through the tree is shown in the following diagram.
Estimate the message length of (@4 of) the data in
the two deepest leaf nodes only.
Show working.
[(c) 5 marks]
- (d) Estimate the change in total message length (both tree and data|tree)
if the two deepest leaves, as identified in part (c),
and the @0 test-node immediately above them
were collapsed to one leaf. Show working.
Should the change be made? Why or why not?
[(d) 5 marks]
[Total: 30 marks]
|