Pore Pressure Diffusion

Roberto Weinberg, Monash University, Australia

 

 

Copyright 2005-2009 by Roberto Weinberg. All rights reserved. Unlimited permission to copy or use is hereby granted for non-profit driven enterprise subject to inclusion of this copyright notice and my World Wide Web URL: users.monash.edu.au/~weinberg. We would very much appreciate an email stating how this material will be used. Thanks, RW.

 

This section explores the diffusion of pore pressure through a FLAC calculation. Because of compressibility of the pore fluids, as measured by the bulk modulus (Kw), an increase in pore pressure in part of the modelled volume, for example through fluid influx (discharge), will gradually propagate through the model. Here, this propagation is explored by studying the evolution of pore pressure in two models with different fluid bulk moduli (Kw), one with the value of water Kw=2.e9, and another three orders of magnitude higher, for comparisson.

 

 

MODELS

The model is a horizontal crustal section at 2 kbar, and a high pore pressure is imposed on the western boundary (1.e7 Pa) and the aim is to track equillibration of the system. Mechanical deformation is turned off.

FLAC input file
Pore pressure distribution after 100 flow time steps. High pore pressure and a steep gradient develop on the western side, but no evidence of that increased pore pressure is recorded on the eastern side. Click on figure to see movie. The diagram on the right-hand-side of the movie is an profile of pore pressure from left to right.

 

 

THE ROLE OF FLUID BULK MODULUS

 

The role of the bulk modulus of the pore fluid here is explored by varying its value in two calculations.

 

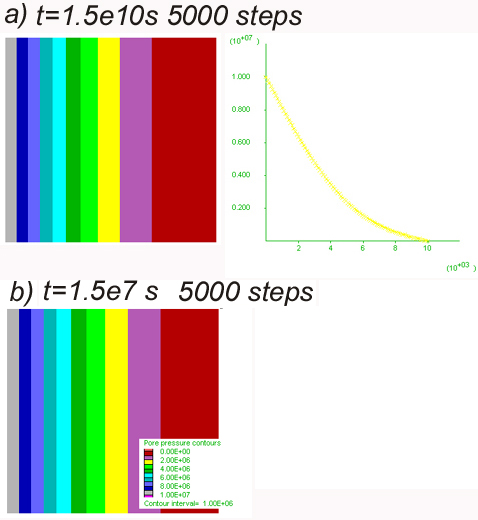
These two images show the results after the same number of calculation steps for two models with different fluid bulk modulus: a) calculation using the bulk modulus of water Kw=2.e9 Pa; b) calculation where the fluid bulk modulus is three orders of magnitude higher than water Kpore=2.e12 Pa. The results are identical, the only difference is a three order of magnitude faster time step for b) due to the higher value of Kpore. This is because the time step is inversely proportional to the Kpore (see FLAC manual).

 

 

IMPLICATIONS AND EFFECTS

The implications are best exemplified by the models presented in wherea rapid increase in pore pressure at the base of the model due to fluid influx, causes yielding of the lower part of the model and releases the stresses in the upper part of the model, leading to fracturing at the base and inhibiting yielding at the top.

If the bulk modulus of the pore fluids used were to be higher, pore pressure would propagate more rapidly across the model, leading to a crustal wide yielding to a generalized pore pressure increase, such as happens late in the model shown above (movie).