Algorithms glossary Sorting Insertion Quick Merge Heap Dutch N.F. Radix |
Heap sort forces a certain property onto an array which makes it into what is known as a heap. The elements of the array can be thought of as lying in a tree structure:
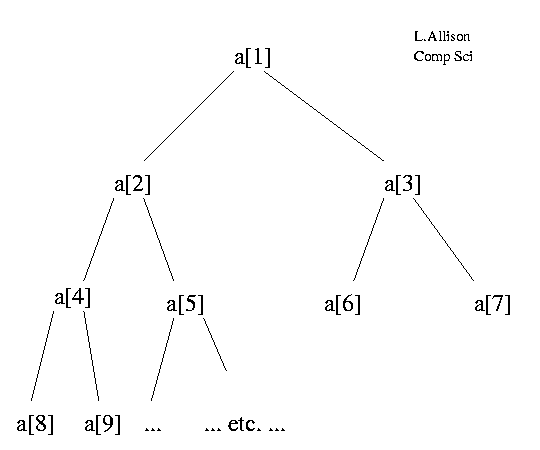
--- Array as a Heap ---
The children of a[i] are a[2*i] and a[2*i+1].
The tree structure is purely notional; there are no pointers etc..
Note that the array indices run through the "nodes"
in breadth-first order,
An array a[i..j] is called a heap if the value of each element is greater than or equal to the values of its children, if any. Clearly, if a[1..N] is heap, then a[1] is the largest element of the array.
Now, if a[k+1..N] is a heap, a[k..N] can be made into a heap efficiently:
downHeap(int a[], int k, int N) /* PRE: a[k+1..N] is a heap */ /* POST: a[k..N] is a heap */ { int newElt, child; newElt=a[k]; while(k <= N/2) /* k has child(s) */ { child = 2*k; /* pick larger child */ if(child < N && a[child] < a[child+1]) child++; if(newElt >= a[child]) break; /* else */ a[k] = a[child]; /* move child up */ k = child; } a[k] = newElt; }/*downHeap*/
This operation moves the new element, a[k], down the heap, moving larger children up, until the new element can be placed in such a way as to maintain the heap property. The heap can have "height" at most log2(N), so the operation takes at most O(log(N)) time.
Heap Sort
This now leads to a version of heap sort known as (bottom-up) heap sort:
heapSort(int a[], int N) /* sort a[1..N], N.B. 1 to N */ { int i, temp; for(i=N/2; i >= 1; i--) downHeap(a, i, N); /* a[1..N] is now a heap */ for(i=N; i > 1; i--) { temp = a[i]; a[i]=a[1]; /* largest of a[1..i] */ a[1]=temp; downHeap(a,1,i-1); /* restore a[1..i-1] heap */ } }/*heapSort*/
Heap Sort Demonstration
Change the data in the HTML FORM below, click `go', and experiment.
The portion of the array that is a heap is
[...]
Exercises
- For a given value of N, e.g. N=6, find input data that maximises the number of comparisons that the algorithm makes.
- For a given value of N, e.g. N=6, find input data that minimises the number of comparisons that the algorithm makes.
Complexity
Time
Heap sort makes at most 1.5*N calls on downHeap. DownHeap makes at most log(N) iterations, and each iteration makes two comparisons, so heap sort makes at most 3*N*log(N) comparisons. It can be shown than bottom up heap sort actually makes at most 2*N*log(N) comparisons. Its worst and average case time-complexity is O(N*log(N)).
Space
Heap Sort's space-complexity is O(1), just a few scalar variables.
Stability
Heap sort is not stable.
Notes
- J. W. J. Williams. Algorithm 232 Heapsort. Comm. of the ACM, 7(6), p347-348, 1964.
- R. Schaffer & R. Sedgewick. The analysis of Heapsort. J. of Algorithms 15, p76-100, 1993.
- On average, Quick sort is faster than Heap sort, but Heap sort is guaranteed to be fast, O(N*log(N)).
- The heap data-structure is also important as a [priority queue], and can be used, for example, in a version of Kruskal's [minimum spanning tree] algorithm.
L. A.©,
Department of Computer Science UWA 1984, Department of Computer Science Monash 1986, and (HTML) School of Comp. Sci. & Software Engineering, Monash University 1999.
|