Research:

My research is in a branch of geometry, called low dimensional topology.

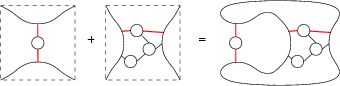
Specifically, I work with 3-manifolds: objects that look like 3-dimensional space when you zoom in far enough. By powerful results proved by Grigori Perelman soon after the turn of the 21st century, every 3-manifold can be cut into pieces that admit a geometry, and the most common geometry is hyperbolic. I look at questions relating hyperbolic geometry to more topological or combinatorial descriptions of 3-manifolds. Here are some questions I have investigated:

  • A knot gives a 3-manifold: the knot complement, by removing the knot from 3-space. Given only a diagram of a knot, what is the hyperbolic volume of the knot? How does it depend on the diagram?

  • Where are the geodesics (the straight lines) in knot diagrams and other simple spaces? Are important arcs in a topological description also geodesic under the geometric description?

  • How complicated can the geometry of a knot complement be? What about knots obtained by topological moves from other knot complements? How are their geometries related?

Related Videos: