Message from Monte Carlo

In previous work (Fitzgibbon, Dowe, and Allison, 2002b,a) we have presented the Message from Monte Carlo (MMC) methodology, a general methodology for performing minimum message length inference using posterior sampling and Monte Carlo integration. In this section we describe the basic elements of the Message from Monte Carlo methodology. These elements will be used in the algorithms given in the following sections.

The basic idea is to partition a sample from the posterior distribution of the parameters into uncertainty regions representing entries in the MML instantaneous codebook. Each region has a point estimate which characterizes the models in the region. The point estimate is chosen as the minimum prior expected Kullback-Leibler distance estimate over the region. The regions are chosen so that the models contained within a region are similar in likelihood and Kullback-Leibler distance (to the point estimate).

Each region also has an associated message length which can be considered as the negative logarithm of the weight attributed to the region. The posterior epitome is the set of point estimates (one for each region) weighted by the antilog of the negative message length.

The message length approximation that is generally used in MMC is Dowe's MMLD minimum message length approximation (Fitzgibbon, Dowe, and Allison, 2002a, section 2.4). Given an uncertainty region of the parameter space, $R$, prior distribution, $h(\theta)$, and likelihood function, $f(x\vert\theta)$, the message length of the region, $R$, is

$$= - \log \left( \int_R h(\theta) \, d\theta \right) - \frac{\int_R h(\theta) \cdot \log f(x\vert\theta) \, d\theta}{\int_R h(\theta) \, d\theta}$$ (4)

for continuous parameter space, or

$$= - \log \left( \sum_{\theta \in R} h(\theta) \right) - \frac{\su... ...eta \in R} h(\theta) \cdot \log f(x\vert\theta)}{\sum_{\theta \in R} h(\theta)}$$ (5)

for discrete parameter spaces⁴.

The MMLD message length equation can be seen to contain two terms. The first term is the negative logarithm of the integral of the prior over the region. It approximates the length of the first part of the MML message (i.e. $-\log p_i$) from Equation 3. The second term is the prior expected negative logarithm of the likelihood function over the region. This approximates the MML message second part and is an average because we do not know the true estimate used in the first part. A shorter message length is to be preferred and involves a trade-off between the first and second terms. Consider a region growing down from the mode in a unimodal likelihood function. As the region grows the first term will decrease (as the integral of the prior increases) but the second term will increase (as the likelihood of the models added to the region decreases). The MMLD message length attempts to take into account the probability mass associated with the region surrounding a point estimate (rather than the point estimate's density for example).

To calculate the MMLD message length we use importance sampling and Monte Carlo integration. We sample from the posterior distribution of the parameters

$$S = \{ \theta_t : t = 1,...,N \}$$ (6)

and then choose a subset of this sample, $Q$, to implicitly define the uncertainty region, $R$. The first part of the message length can then be approximated by

$$\approx -\log \left( \frac{ \frac{1}{N} \sum_{\theta \in Q} h(\th... ...\in Q} f(x\vert\theta)^{-1}}{\sum_{\theta \in S} f(x\vert\theta)^{-1} } \right)$$ (7)

where $I(.)$ is the importance sampling distribution (here we use the posterior, $I(\theta) \propto h(\theta) f(x\vert\theta)$). This estimate does not require that the prior, $h(.)$, or the importance sampling distribution be normalised.

The second part is approximated using

$$\approx - \frac{ \sum_{\theta \in Q} h(\theta) I(\theta)^{-1} \lo... ...rt\theta)^{-1} \log f(x\vert\theta) }{\sum_{\theta \in Q} f(x\vert\theta)^{-1}}$$ (8)

These estimates allow the message length to be approximated for some $Q$. We now discuss how to select the $Q$ that minimises the message length. We first note that if we attempt to minimise Equation 4 we get the following boundary rule

$$- \log f(x\vert\theta) \Bigl\lvert_{\theta \in \partial R} = - \f... ...t_R h(\theta) \log f(x\vert\theta) \, d\theta}{\int_R h(\theta) \, d\theta} + 1$$ (9)

where the boundary, $\partial R$, of $R$, is an iso-likelihood contour of $f$. In other words, the values of $f(x\vert\theta)$ and of $\log f(x\vert\theta)$ are constant on $\partial R$. This boundary rule states that for the region which minimises the message length, the negative log-likelihood at the boundary of $R$ is equal to the prior expected negative log-likelihood over the region plus one. The right hand side can be approximated using Equation 8.

For the discrete version of MMLD (Equation 5) the boundary rule (Equation 9) is only an approximation and has the following error

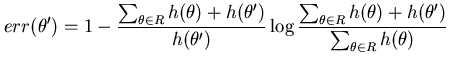$$err(\theta') = 1 - \frac{\sum_{\theta \in R} h(\theta) + h(\theta... ...frac{\sum_{\theta \in R} h(\theta) + h(\theta')}{\sum_{\theta \in R} h(\theta)}$$ (10)

which involves only the prior.

Since the posterior sampling process has discretised the space we will need to include the $err$ term for both discrete and continuous parameter spaces. We can estimate the $err$ term using

$$err(\theta') \approx 1 - \frac{\sum_{\theta \in Q} f(x\vert\theta... ...{-1} + f(x\vert\theta')^{-1}}{\sum_{\theta \in Q} f(x\vert\theta)^{-1}} \right)$$ (11)

Due to the use of importance sampling the prior terms have cancelled and the estimate does not directly involve the prior. Intuitively we see that $err$ is largest when $Q$ is small and therefore $err$ will have the largest effect when the region is initially being formed.

Selection of the optimal region is simple in the unimodal likelihood case since we can order the sample in descending order of likelihood, then start at the element with maximum likelihood and continue to grow the region accepting models into the region that pass the boundary rule test

$$\theta \in Q -\log f(x\vert\theta) \le - \frac{\sum_{\theta \in Q} \log f(x\ve... ...vert\theta)^{-1} }{\sum_{\theta \in Q} f(x\vert\theta)^{-1} } + 1 - err(\theta)$$ (12)

Such an algorithm is given in the next section. This idea can be similarly extended to the multimodal likelihood case by using order statistics to restrict the regions to be simply connected (briefly discussed in Section 5). For variable dimension posteriors we need a different strategy. We must ensure that regions contain models that are close to the point estimate in Kullback-Leibler distance. This is discussed, and an algorithm given, in Section 6. Now we briefly discuss how to choose the point estimate for a region.

The Point Estimate

Once the region that minimises the message length is found we need to find a point estimate for the region. Staying true to the compact coding approach we use the minimum prior expected Kullback-Leibler distance estimate since this corresponds to the MMLA estimate (see (Fitzgibbon, Dowe, and Allison, 2002a)[section 2.4.1]). This estimate represents a compromise between all of the models in the region and can be considered to be a characteristic model that summarises the region. The prior expected Kullback-Leibler (EKL) distance is

$$E_{h(\theta)}\left[ KL(\theta,\hat{\theta}) \right] = \int_R h(\theta) KL(\theta,\hat{\theta}) \, d\theta$$ (13)

$$\approx \frac{\sum_{\theta \in Q} f(x\vert\theta)^{-1} KL(\theta,\hat{\theta})}{\sum_{\theta \in Q} f(x\vert\theta)^{-1}}$$ (14)

The MML estimate is the $\hat{\theta}$ that gives the minimum EKL distance

$$\hat{\theta} = argmin_{\hat{\theta} \in R} E_{h(\theta)} \left[ KL(\theta,\hat{\theta}) \right]$$ (15)

This estimate could be found by simulation (see, e.g. (Dowe, Baxter, Oliver, and Wallace, 1998) - note that they use the posterior expectation). It could also be found directly using Newton-Raphson type algorithms (as used in the next section). Both of these require that we know the parametric form of the estimate - making them less desireable for use with variable dimension posteriors. An alternative that does not have such a requirement is to find the element of $Q$ that has the minimum EKL distance. This algorithm was used in the MMC algorithm from (Fitzgibbon, Dowe, and Allison, 2002a)[section 3.4]. An exhaustive search (i.e. $argmin_{\hat{\theta} \in Q} E_{h(\theta)} \left[ KL(\theta,\hat{\theta}) \right]$), using Equation 14, requires quadratic time in $\vert Q\vert$ although simple strategies can be employed to reduce this considerably.

In practice it is often beneficial to use the posterior expected Kullback-Leibler distance

$$E_{h(\theta)f(x\vert\theta)}\left[ KL(\theta,\hat{\theta}) \right] = \frac{\int_R h(\theta) f(x\vert\theta) KL(\theta,\hat{\theta}) \, d\theta}{\int_R h(\theta) f(x\vert\theta) \, d\theta}$$ (16)

$$\approx \frac{1}{\vert Q\vert} \sum_{\theta \in Q} KL(\theta,\hat{\theta})$$ (17)

since the Monte Carlo estimate is better behaved.